Fausto Pucheta Fortin
Data Enthusiast | Data Practitioner

Feature Engineer
Principles for better data preprocessing
Table of Contents
a. Categorical Encoding Techniques
b. Numerical Scaling and Transformation
c. Feature Creation and Interaction
d. Temporal and Time-Series Features
1. What is Feature Engineer?
Feature engineer is the act of extracting features from raw data and transforming them into formats that are suitable for a machine learning model.

(Image source: Feature Engineer for Machine Learning. Alice Zheng & Amanda Casari. 2018)
2. Why is so important?
It's a crucial step since the right features ease the difficulty of modeling, enabling to a higher quality output from the data pipeline.
The following are some key aspects that feature engineer can bring to the table:
Enhance Model Performance: well-engineered features, tailored to the specific machine learning problem and algorithm compatibility, significantly impact the performance of models and relevance for the intended task, leading to a more accurate and robust predictions.
Dimensionality Control: they mitigate tu curse of dimensionality, reducing the risk of overfitting, computational inefficiency, and model complexity.
Interpretability: by highlighting meaningful relationships between input variables and the target, they can enhance the interpretability of the model, fostering deeper insights into data patterns.
Utilization of Domain Knowledge: incorporating domain expertise ensures that the created features capture relevant information aligning with real-world phenomena.
Data Quality Improvement: feature engineer addresses missing values, outliers, and noise, leading to a cleaner and more reliable data for analysis and modeling.
Generalization and Transferability: they can still generalize across diverse dataset and scenarios, capturing underlying patterns that extend beyond the original data.
3. Techniques & Procedures
Feature Engineering encompasses a spectrum of techniques, each tailored to specific data characteristics and modeling objectives.
a. Categorical Encoding Techniques
Categorical encoding is a pivotal feature engineering process that transforms categorical data into numerical form, enabling machine learning algorithms to process them effectively.
They can be:
One-hot Encoding:
Creates binary columns for each category. Columns can have 0 or 1.

(Image source:https://www.statology.org/wp-content/uploads/2021/09/oneHot1-768x357.png)
Advantages:
a. Keeps categorical information distinct and non-ordinal.
b. Well-suited for algorithms that work well with binary inputs.
Disadvantages:
a. Increases dimensionality significantly, especially with high-cardinality features.
b. Can lead to multicollinearity (correlation between encoded columns).
Use Cases:
Nominal categories without inherent order, like colors, countries, or genres.
Label Encoding:
Assigns an arbitrary unique integer to each category. The assigned integers do not hold any inherent meaning.

(Image source:https://www.statology.org/wp-content/uploads/2022/08/labelencode2-1-768x475.jpg)
Advantages:
a. Simple and memory-efficient, suitable for large datasets.
b. Can work well with algorithms that can learn ordinal relationships.
Disadvantages:
a. Introduces ordinality that might not exist in the original data.
b. Can mislead algorithms into inferring non-existent relationships.
Use Cases:
Ordinal categories with clear ranking, such as education levels or socio-economic classes.
Ordinal Encoding:
Ordinal Encoding assigns integers based on a predefined order or ranking of categories. The assigned integers reflect the order's hierarchy.

(Image source:https://www.renom.jp/notebooks/tutorial/preprocessing/category_encoding/renom_cat_onehot.png)
Advantages:
a. Preserves ordinal relationships from in the original data.
b. Great informative input to algorithms that understand ordinality.
Disadvantages:
a. Assumes uniform gaps between categories, which may not hold true.
b. Limited flexibility when categories do not have a clear rank.
Use Cases:
Ordinal data where categories have a meaningful order, like star ratings or employment levels.
b. Numerical Scaling and Transformation
Numerical features often vary across different scales and distributions, which can affect the performance of machine learning algorithms. Scaling and transforming these features is a critical aspect of feature engineering that ensures uniformity and enhances model accuracy.
They can be:
Min-Max Scaler:
Transforms numerical features to a common range, usually [0, 1]. It subtracts the minimum value and divides by the range (max - min).

Advantages:
a. Preserves the original data distribution.
b. Suitable for algorithms sensitive to feature scales.
Disadvantages:
a. Sensitive to outliers, which can distort scaling.
b. May not work well with sparse data or outliers.
Use Cases:
Features where preserving the relative relationships is important, like coordinates or pixel values.
Standard Scaling (z-score Normalization):
Transforms features to have a mean of 0 and a standard deviation of 1. It subtracts the mean and divides by the standard deviation.

(Image source:https://developers.google.com/static/machine-learning/data-prep/images/norm-z-score.svg)
Advantages:
a. Centers data around zero, aiding algorithms with symmetric assumptions.
b. Suitable for algorithms like K-Means and SVM that rely on distances.
Disadvantages:
a. Not suitable for algorithms that assume feature ranges, like decision trees.
b. Can be affected by outliers.
Use Cases:
Algorithms sensitive to distances and centered data, such as clustering and Gaussian processes.
Logarithmic Transformation:
Logarithmic transformation applies the logarithm function to numerical features. It helps to reduce the impact of skewed data distributions.

(Image source:https://www.medcalc.org/manual/images/logtransformation.png)
Advantages:
a. Mitigates the influence of extreme values and outliers.
b. Can improve the performance of algorithms that assume normality.
Disadvantages:
a. Cannot handle zero or negative values, requiring preprocessing.
b. May not be suitable for all types of skewed distributions.
Use Cases:
Features with highly skewed distributions, like income or population data.
c. Feature Creation and Interaction
Creating new features and capturing interactions between existing ones can amplify the predictive power of machine learning models.
They can be:
Polynomial Features:
Involves generating new features by raising existing ones to different powers. For example, transforming a feature 'x' into 'x^2'.

(Image source:https://miro.medium.com/v2/resize:fit:720/format:webp/1*jF362YOYhve5djg7iHJ-Dw.png)
Advantages:
a. Captures nonlinear relationships between features and the target.
b. Enables models to represent complex interactions.
Disadvantages:
a. Rapidly increases dimensionality with higher degrees.
b. May lead to overfitting if not applied judiciously.
Use Cases:
a. Modeling phenomena with nonlinear trends, like physical processes governed by polynomial
equations.
b. Capturing curvature in scatterplots that do not follow linear patterns.
Interaction Features:
Interaction features are derived by combining two or more existing features through arithmetic operations like addition, subtraction, or multiplication.

(Image source: https://miro.medium.com/v2/resize:fit:720/format:webp/1*m5NTDYNDzq7j12SWQZvPhw.jpeg)
Advantages:
a. Reveals nuanced relationships between features.
b. Empowers models to incorporate context-dependent insights.
Disadvantages:
a. Requires domain knowledge to identify meaningful interactions.
b. Can lead to high-dimensional feature spaces.
Use Cases:
a. Modeling situations where two or more features jointly influence the target, like revenue from a
product sale.
b. Capturing how product attributes interact to affect consumer preferences.
Domain-Specific Feature Generation:
Domain expertise can guide the creation of features that are highly relevant to the problem at hand.

Advantages:
a. Incorporates specific knowledge about the problem domain.
b. Enhances model accuracy by including relevant information.
Disadvantages;
a. Relies on accurate domain knowledge, which might not always be available.
b. Can introduce subjectivity if not carefully curated.
Use Cases:
Incorporating specific metrics or ratios that are crucial within a particular domain, such as medical
diagnostics or quality control in manufacturing.
d. Temporal and Time-Series Features
Temporal data, characterized by its chronological nature, requires specialized techniques for effective feature engineering. They allow harnessing the patterns embedded within time-dependent data.
Time-Based Features:
Involve extracting relevant components from timestamps, such as day of the week, month, year, etc.

(Image source: https://qph.cf2.quoracdn.net/main-qimg-738f6b89f3fafc6be4b36fafd9efcf60)
Advantages:
a. Enables models to capture periodic and seasonal patterns.
b. Provides context that correlates with real-world events and behaviors.
Disadvantages:
a. Selecting appropriate time components requires domain understanding.
b. Multiple time components can increase feature dimensionality.
Use Cases:
Capturing seasonality in retail sales during holidays, identifying weekly trends in social media activity,
and modeling monthly patterns in energy consumption
Lag Features:
Incorporate past observations of a variable as features for predicting its future values. E.g.: using
yesterday's stock price to predict today's price.

(Image Source: https://storage.googleapis.com/kaggle-media/learn/images/Hvrboya.png)
Advantages:
a. Integrates memory of previous states, crucial for time-series forecasting.
b. Captures autocorrelation and dependencies over time.
Disadvantages:
a. Determining optimal lag lengths requires experimentation and domain knowledge.
b. Including excessive lags can introduce multicollinearity.
Use Cases:
Forecasting financial indicators like stock prices, predicting weather conditions based on historical data,
and anticipating future product demand.
Rolling Statistics:
Compute aggregate measures (e.g., mean, standard deviation) over a moving window of time,
smoothing out noise and revealing trends.
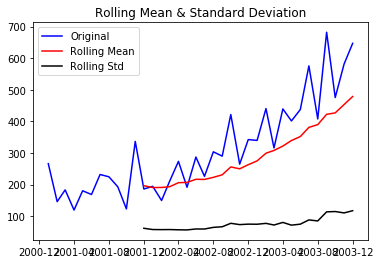
(Image Source: https://cdn-images-1.medium.com/max/800/1*cYq5bwsut0V0Jn2jFWISFQ.png)
Advantages:
a. Filters out short-term fluctuations, exposing underlying patterns.
b. Helps identify anomalies and changes in behavior.
Disadvantages:
a. Choosing an appropriate window size requires domain knowledge and experimentation.
b. Data loss occurs at the edges of the time series due to window constraints.
Use Cases:
Analyzing financial data to spot short-term trends in stock prices, monitoring sensor readings to detect
irregularities, and enhancing web analytics by reducing noise from user activity data.
e. Textual Feature Extraction
Textual feature extraction techniques enable you to convert words and sentences into structured data that algorithms can understand. They can be as follow:
TF-IDF (Term Frequency-Inverse Document Frequency):
Computes a numerical value for each word in a document, indicating its importance relative to the entire corpus. It considers both the frequency of a word (term frequency) and its rarity across the entire corpus (inverse document frequency).

Advantages:
a. Highlights significant words while downplaying common ones.
b. Effective for document similarity, text categorization, and information retrieval.
Disadvantages:
a. Ignores word order and context.
b. Not suitable for capturing semantic relationships.
Use Cases:
Document classification, content recommendation, and
sentiment analysis.
Word Embeddings (Word2Vec, GloVe):
Represent words as dense vectors in a continuous space, capturing semantic relationships. Word2Vec and GloVe are popular methods for creating word embeddings.

(Image Source: http://jalammar.github.io/images/word2vec/word2vec.png)
Advantages:
a. Preserves semantic meaning and relationships between words.
b. Effective for tasks involving word similarity, sentiment analysis, and named entity recognition.
Disadvantages:
a. Requires large amounts of training data to learn meaningful embeddings.
b. May not capture domain-specific or context-dependent meanings.
Use Cases:
Natural language processing tasks like machine translation, chatbots, and text generation.
Text Preprocessing (Tokenization, Lemmatization):
Involves breaking text into smaller units (tokenization) and reducing words to their base or root form (lemmatization) to standardize the text data.

(Image Source: https://ambrapaliaidata.blob.core.windows.net/ai-storage/articles/image_oJ2qFRU.png)
Advantages:
a. Reduces vocabulary size, simplifying analysis.
b. Enhances the quality of word-based features.
Disadvantages:
a. May not handle domain-specific vocabulary well.
b. Loss of some context and information during lemmatization.
Use Cases:
Cleaning and preparing text data for further analysis and modeling.
f. Dimensionality Reduction
Dimensionality reduction techniques enable us to retain essential information while reducing the number of features, enhancing model performance and interpretability. In those cases we use:
PCA (Principal Component Analysis):
Identifies orthogonal axes (principal components) that capture the maximum variance in the data. It projects the data onto these components to reduce dimensionality.

(Image Source: https://knowledge.dataiku.com/latest/_images/stats-PCA-example.png)
Advantages:
a. Minimizes information loss by preserving variance.
b. Enhances model efficiency and reduces overfitting.
Disadvantages:
a. Assumes that high-variance directions are important, which might not always hold.
b. May not perform well on non-linear data distributions.
Use Cases:
Visualizing high-dimensional data, preprocessing for downstream algorithms, and noise reduction.
Linear Discriminant Analysis (LDA):
LDA seeks linear combinations of features that maximize class separation. It's often used for classification tasks.

Advantages:
a. Maximizes class separability while reducing dimensionality.
b. Focuses on preserving inter-class distances and minimizing intra-class distances.
Disadvantages:
a. Assumes that the data is normally distributed and that classes have equal covariance matrices.
b. LDA might not be optimal for all classification problems.
Use Cases:
Pattern recognition, classification, and improving model efficiency.
T-Distributed Stochastic Embedding (t-SNE):
Is a non-linear dimensionality reduction technique that focuses on preserving pairwise similarities
between data points in the high-dimensional space when projecting to a lower-dimensional space.

(Image Source: https://miro.medium.com/v2/resize:fit:720/format:webp/1*P7xpVKDJfO9k4of2n5tfoQ.png)
Advantages:
a. Captures complex relationships and non-linear structures.
b. Particularly useful for visualizing high-dimensional data clusters.
Disadvantages:
a. Interpretability can be challenging due to its non-linear nature.
b. Sensitive to different choices of hyperparameters.
Use Cases:
Cleaning and preparing text data for further analysis and modeling.
4. Good Practices
Feature engineering is a delicate art that requires a balance of creativity, domain knowledge, and technical expertise. Adopting good practices ensures that your engineered features are not only effective but also reliable, robust, and well-suited for the task at hand.
Here are some tips:
Understand your data:
Thoroughly understand your data's domain, context, and intricacies. Domain expertise helps you identify relevant features and avoid introducing biases.
Start Simple:
Begin with basic features and build complexity gradually. Simple features often provide substantial predictive power and are less prone to overfitting.
Data Cleaning and Preprocessing:
Ensure your data is clean and well-preprocessed before feature engineering. Handle missing values, outliers, and data inconsistencies to create a solid foundation.
Explore Data Relationships:
Analyze how features interact with the target variable and each other. Visualizations, statistical tests, and domain knowledge can help uncover important relationships.
Feature Importance and Selection:
Utilize techniques like feature importance scores and recursive feature elimination to identify the most impactful features for your model.
Avoid Data Leakage:
Feature engineering should be done only on the training data. Any transformations applied to the test data must mimic those performed on the training set to avoid data leakage.
Domain-Specific Features:
Incorporate features derived from domain knowledge to enhance model interpretability and accuracy. These features can capture nuances specific to your problem.
Domain Adaptation:
Be aware of potential domain shifts when deploying models to new environments. Feature engineering might need adjustments to accommodate differences.
Documentation:
Keep track of the features you engineer, the rationale behind them, and any transformation processes. Documentation helps ensure reproducibility and transparency.
Monitoring and Maintenance:
As your model is deployed and new data streams in, continuously monitor the performance of your features and update them as needed.
Iteration and Experimentation:
Feature engineering is an iterative process. Experiment with different features, transformations, and combinations to find the best-performing set.
5. Conclusion
Feature engineering, the bridge between raw data and predictive models, is a blend of creativity and precision. From encoding categorical variables to crafting temporal insights, we've explored techniques that distill data's essence. This journey then, can be resumed in the following insights:
1. Depth Through Techniques
Feature engineering techniques add layers of depth and complexity to the data enabling more meaningful and insightful information. They go beyond the surface-level uncovering hidden patterns and relationships not immediately apparent.
2. Significance of Context
Crafting effective features requires aligning with the problem's context. Understanding the domain ensures that features resonate with the real-world intricacies, enhancing model interpretability and accuracy.
3. Iterative Journey
Feature engineering isn't a one-time affair. It thrives on experimentation, iteration, and feedback loops. Exploring various techniques and evaluating their impact empowers feature selection that truly amplifies model performance.
6. References
Géron, A. (2019). Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow. O'Reilly Media.
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., ... & Vanderplas, J. (2011). Scikit-learn: Machine learning in Python. Journal of Machine Learning Research.
McKinney, W. (2017). Python for Data Analysis. O'Reilly Media.
Chollet, F. (2017). Deep Learning with Python. Manning Publications.
Brownlee, J. (2020). Feature Engineering for Machine Learning. Machine Learning Mastery.
Jurafsky, D., & Martin, J. H. (2019). Speech and Language Processing. Pearson.



